Pow(x, n)
- https://leetcode.com/explore/interview/card/top-interview-questions-medium/113/math/818/
- 분류: Top Interview Questions - Medium - Math
문제
- x의 n승을 계산하는 pow(x, n)을 구현하라.
- type x: float, type n: int, rtype: float
예시
Example 1:
Input: x = 2.00000, n = 10
Output: 1024.00000
Example 2:
Input: x = 2.10000, n = 3
Output: 9.26100
Example 3:
Input: x = 2.00000, n = -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25
조건
- 100.0 < x < 100.0
- 231 <= n <= 2311
- n is an integer.
- 10^4 <= x^n <= 10^4
풀이
1. 제곱 연산자 ** 사용 / pow() 함수 사용
def myPow(self, x, n):
return x ** n
def myPow(self, x, n):
return pow(x, n)
# 혹은 아예 pow 함수 대입
myPow = pow
Time: O(n) / Space: O(1)
Runtime: 23 ms (beats 23.97%) / Memory Usage: 13.3 MB (beats 92.57%)
함수를 구현하라는 문제에 이미 구현된 연산자나 함수를 쓰는게 올바른 접근은 아니라는 것을 우리 모두가 알 것이다.
그래서 Binary Exponentiation을 이용한 풀이를 소개한다.
Binary Exponentiation
직역하면 이진 지수화로, 거듭제곱 연산을 O(log n) 시간 복잡도로 수행할 수 있는 알고리즘이다.
지수를 이진수로 표현하는 것을 통해 거듭제곱 연산을 쪼개서 수행하는 것이 기본 아이디어다.
지수를 이진수로 변환한 후 3^1을 3^2 계산에 이용하고 3^2 계산을 3^4 계산에 이용하는 등 연산을 쪼개는 방법을 통해 연산 수를 줄여 시간 복잡도를 낮춘다는 말이다.
기본 아이디어
101100 이런 식의 이진수가 있을 때 맨 뒷 비트(0)부터 처리함 - 비트 처리 위해 홀/짝 확인 (맨 뒷 비트가 0인지 1인지 확인)

적용 예시
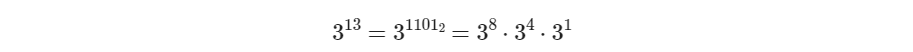


2. 비트 연산을 이용한 반복문 (Binary Exponentiation)
단순히 O(n)의 반복문을 돌리면 메모리 초과 에러가 나므로 다른 방법이 필요함 → Binary Exponentiation
코드 구조
- n을 이진수로 변환했을 때 맨 뒤의 비트부터 검사
- n이 음수라면 x를 1/x로 만들고 n의 부호를 뒤집어줌
- n&1 또는 n%2로 현재 맨 뒤 비트가 1인지 검사 → 1이라면 x를 곱해줌 (해당 비트가 0이면 곱할 필요 없음)
- 다음 비트 연산을 수행하기 위해 x *= x로 x값을 갱신해줌
- n >>= 1 또는 n = n // 2로 다음 비트로 이동
class Solution:
def myPow(self, x, n):
if n < 0:
x = 1 / x
n = -n
pow = 1
while n:
if n & 1: # if n % 2:
pow *= x
x *= x
n >>= 1 # n = n // 2
return pow
Time: O(logn) / Space: O(1)
Runtime: 15 ms (beats 80.35%) / Memory Usage: 13.3 MB (beats 72.50%)
3. 재귀 호출 (Binary Exponentiation)
마찬가지로 binary exponentiation을 이용한 풀이로 n이 홀수일 때 / 짝수일 때 연산을 다르게 수행하도록 구성한다.
아래 아이디어와 로직이 동일하다.
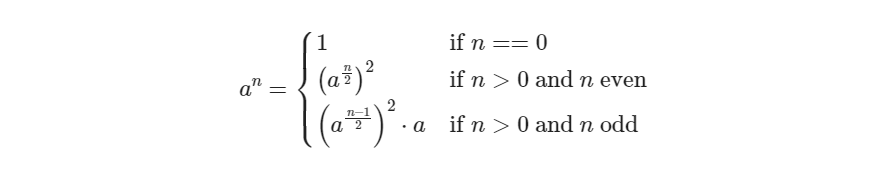
class Solution:
def myPow(self, x, n):
if not n:
return 1
if n < 0:
return 1 / self.myPow(x, -n)
if n % 2: # n이 홀수면
return x * self.myPow(x, n-1)
return self.myPow(x*x, n/2) # n이 짝수면
Time: O(logn) / Space: O(logn)
Runtime: 19 ms (beats 52.73%) / Memory Usage: 13.4 MB (beats 72.5%)
시간복잡도는 같지만 일반적으로 그렇듯이 재귀가 반복문보다 느린걸 확인할 수 있다.
'알고리즘 > 리트코드 LeetCode' 카테고리의 다른 글
| [리트코드 LeetCode] Generate Parentheses (Python) (0) | 2023.04.24 |
|---|---|
| [리트코드 LeetCode] Sqrt(x) (Python) (1) | 2023.04.20 |
| [리트코드 LeetCode] Excel Sheet Column (Python) (0) | 2023.04.19 |
| [리트코드 LeetCode] Factorial Trailing Zeroes (Python) (0) | 2023.04.19 |
| [리트코드 LeetCode] Happy Numebr (Python) (0) | 2023.04.18 |
